Topological stability and textual differentiation in human interaction networks:
statistical analysis, visualization and linked data
Advisor: Prof. Dr. Osvaldo Novais de Oliveira Junior
Candidate: Renato Fabbri
Doctoral thesis defense in Computational Physics, May/08/2017
São Carlos Institute of Physics, University of São Paulo





Outline
- Introduction
- complex and human interaction networks
- text mining, visualization, linked data
- Materials and methods
- data from email and other sources
- circular statistics of temporal activity
- complex networks: metrics, PCA and Erdös Sectioning
- text mining: adaptation of the Kolmogorov-Smirnov test, Wordnet
- Results and discussion
- topological stability
- textual differentiation
- Versinus method for evolutive network visualization
- Linked Open Social Database
- other results
- Conclusions and further work
1
Outline
How stable are the scale-free and other topological features in social networks? How does text and topology relate in social interaction networks?
These questions are important for us to characterize our social systems.
We relied in the literature and data mining to reach two main results presented in this work:
- The stability of the networks with respect to hubs, intermediary and peripheral participants, to PCA formation of the components and to circular statistics of activity along time.
- Differentiation of linguistic features from hubs, intermediary and peripheral participants.
There are subsidiary results in dynamic graph visualization and linked data. They enabled and shaped the core analysis.
2
Introduction
3
Introduction
4
Introduction
There are \(10^{80}\) atoms in the observable universe, a scale reference. Consider \(N\) the number of individuals needed to yield more possible networks than atoms in the universe. Each edge is a Bernoulli variable: the edge may be present or not.
I.e. only 24 vertices are needed for there to be more possible networks than atoms in the universe. This endorses the utility of paradigms for networks, and of generic measures for each vertex and for the network, instrumental for complex networks, including human interaction networks.
Complex System \(\Rightarrow\) consists of several parts whose interaction exhibits emerging behavior. It is usual to consider that a complex system: processes information, exhibits adaptive mechanisms, may have reproduction capabilities. A complex system is integrated with other complex systems and the environment in which it subsists.
5
Introduction
- Complex networks
- Text mining
- Network visualization
- Linked data
- Social participation
- Programming, APIs and protocols
- Art
6
Materials
- Emails from the Gmane database
- Data from:
- IRC
- Cidade Democrática
- ParticipaBR
- Algorithmic Autoregulation (AA)
7
Methods
These are the methods considered for studying the topology of the systems:
- Interaction networks attainment
- PCA of topological metrics
- Erdös sectioning
The core method used to observe textual differences in the Erdös sectors is an adaptation of the Kolmogorov-Smirnov test.
For enabling the research, we had to use methods for:
- Audiovisualization of networks
- Linked representation of data
- Typological and humanistic considerations
Directional statistics (or spherical or circular statistics) are generic for observations in Riemannian manifolds and was used to observe the distribution of sent times from email messages.
8
Circular statistics
Consider each measure over time:
The norm and angle of the moments:
The angle is measure of localization and the dispersion is given by:
We also used \(\frac{b_h}{b_l}\) between the largest \(b_h\) and the smallest \(b_l\) incidence in the histograms.
9
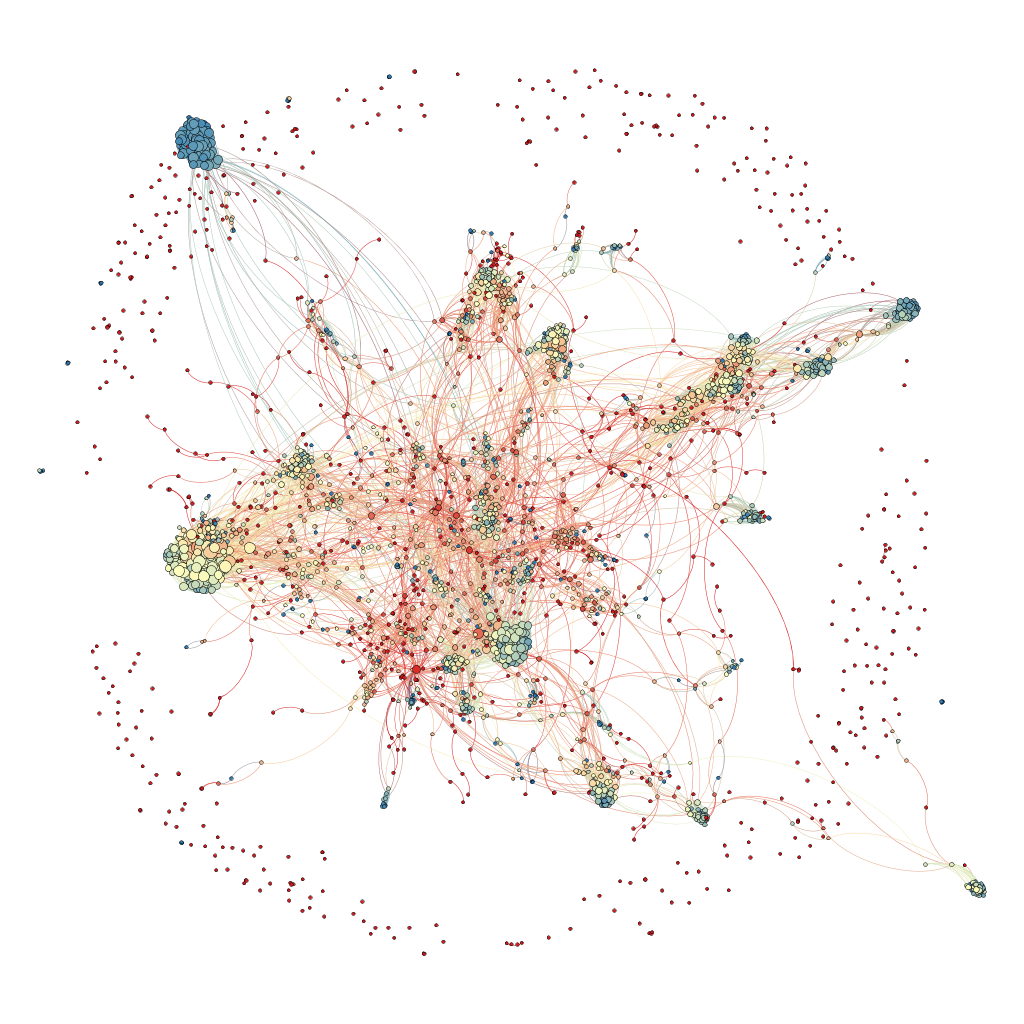
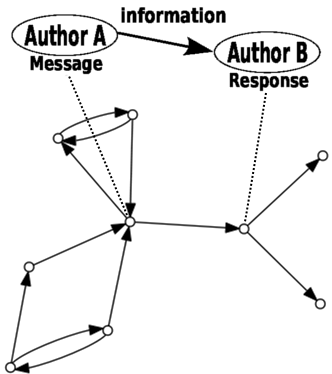
Interaction networks attainment
10
Erdös sectioning
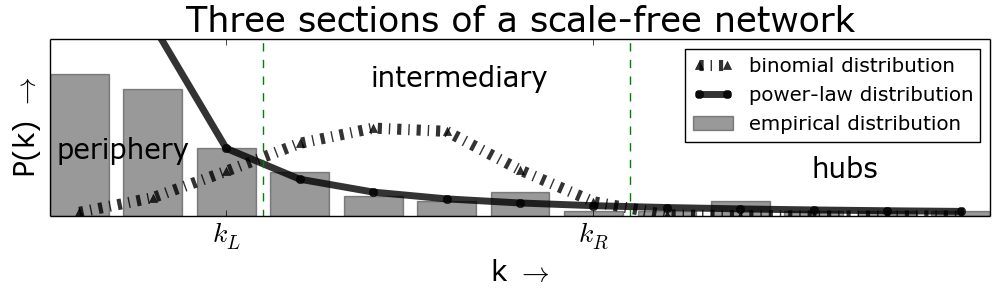
where
11
PCA in topological metrics
Mean and standard deviation of measurements j in eigenvectors k through all l instances and of eigenvalues k through all l instances:
\begin{eqnarray} \mu_{V'}[j,k] &=\frac{\sum_l^L V'[j,k,l]}{L}\nonumber\\ \sigma_{V'}[j,k]&=\sqrt{\frac{(\mu_{V'}-V'[j,k,l])^2}{L}}\\\nonumber \mu_{D'}[k]&=\frac{\sum_l^L D'[k,l]}{L}\\\nonumber \sigma_{D'}[k]&=\sqrt{\frac{(\mu_{D'}-D'[k,l])^2}{L}} \end{eqnarray}
We used standard measures of (in, out, total-) degree, (in, out, total-) strength, betweenness centrality and clustering coefficient. We also used non-standard measures of asymmetry and disequilibrium.
12
Adaptation of the Kolmogorov-Smirnov two sample test
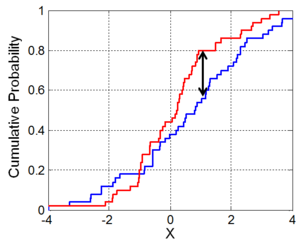
| α | 0.1 | 0.05 | 0.025 | 0.01 | 0.005 | 0.001 |
|---|---|---|---|---|---|---|
| c(α) | 1.22 | 1.36 | 1.48 | 1.63 | 1.73 | 1.95 |
13
Audiovisualization of data
14
Linked data representations and ontologies
To enable our research start a social dataset which fits our needs, we developed:
- translation of relational data into RDF by means of Python scripts.
- Formalization of social participation instances and mechanisms in OWL
We maintained online infrastructure to navigate and query the linked data for some months. USP cloud services started charging so we had to withdraw these services.
15
Typological and humanistic considerations
- Our networks are constituted by human beings.
- Prejudice factors.
- The environment in which the network is observed.
- (Percolatory) Experiments and performances in social systems.
- Anthropological physics.
16
Results
- Temporal and topological stability.
- Textual differentiation.
- Initialization of the (Brazilian) social participation data cloud.
- The Versinus dynamic graph visualization method.
- Software development.
17
Temporal and topological stability
- Circular statistics are about the same in every email list and in all scales from seconds to semesters.
- Fixed fractions of participants in each of the Erdös sectors, in accordance with the literature. This might be the first use of the method and verification of the consistency of the hubs, intermediary and peripheral sectors.
- Stability of the principal components (PCA).
- Human typology from Erdös sectors.
18
Temporal and topological stability
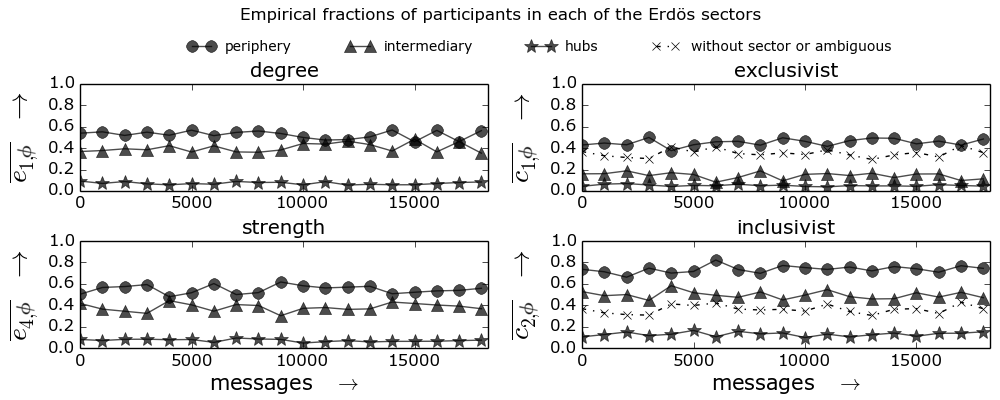
19
Temporal and topological stability
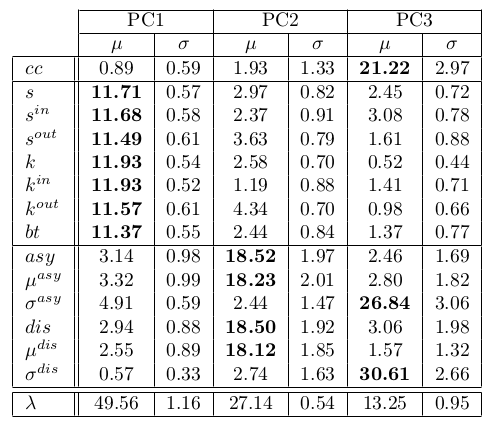
20
Temporal and topological stability
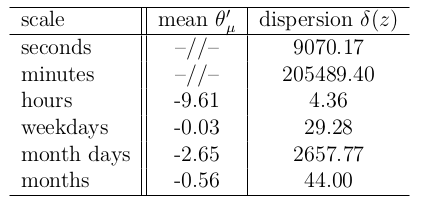
21
Temporal and topological stability
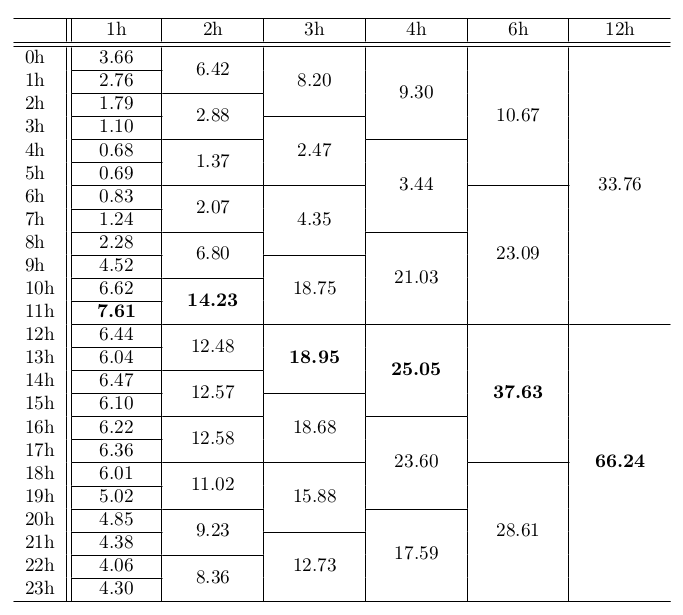
22
Textual differentiation
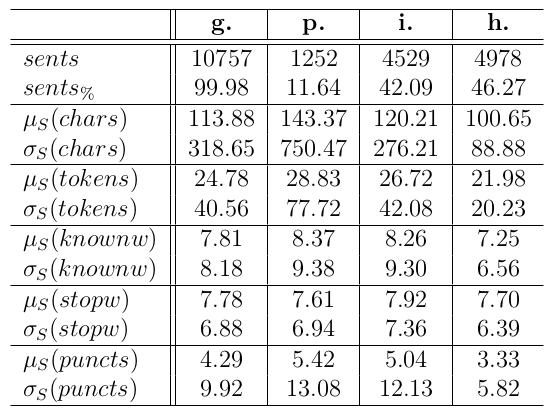
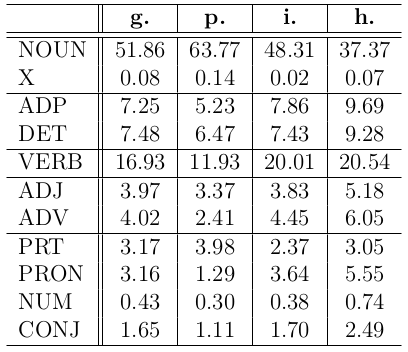
- The texts produced by each of the Erdös sectors are extremely different. The differences found are greater than between different networks or between the same sector of different networks.
- The differences are sometimes evident: hubs use smaller words, sentences and messages. Peripherals use more nouns and less adjectives.
- Correlations of topological and textual measurements do not present trivial patterns.
- Principal components are mainly of textual or topological metrics; the merge of these different sets of metrics is modest.
- Persistence of the differences in incident and existent words.
23
Textual differentiation
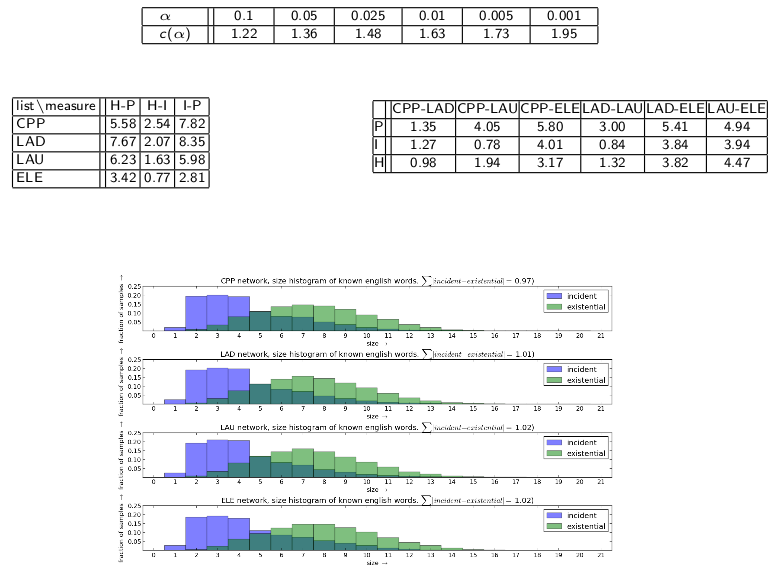
24
Textual differentiation
25
Audiovisualization with Versinus
In Versinus (Latim versus+sinus meaning line+sinusoid), the Erdös sectors are positioned on the first and second half of the sinusoid and on the upper line. Vertex size corresponds to in and out strengths. Color corresponds to clustering coefficient. Music is synthesized using the total activity of the four most active hubs.
26
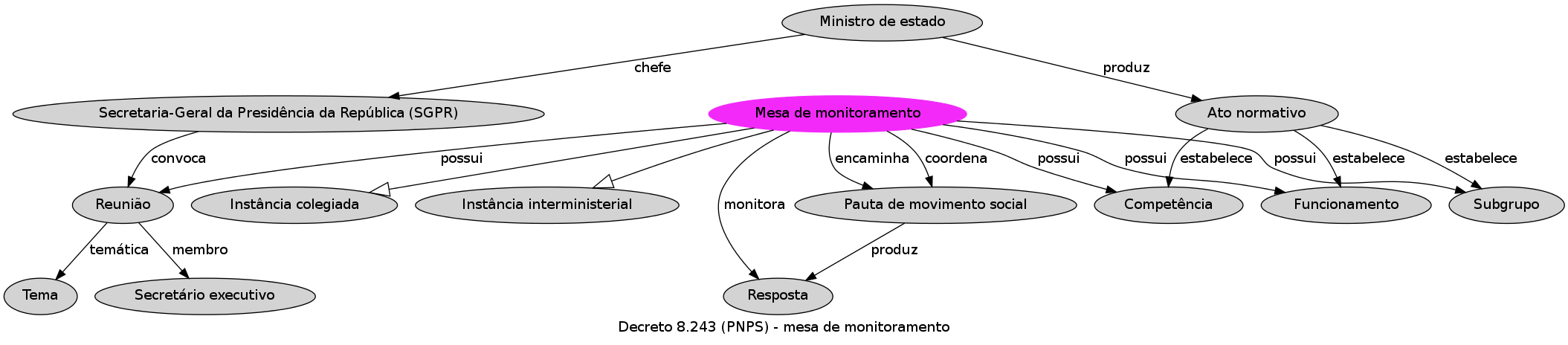
Linked social data
- Formalizations of ontologies (OWL) and vocabularies (SKOS) of social structures. OPS, OPA, OPP, Ontologiaa, OCD, OBS, VBS.
- Python scripts for translating relational data into RDF.
- Data-oriented ontology synthesis method.
27
Art and sensory mappings
- Four hubs dance. Social prelude.
- Versinus.
- Other pieces: online app (PHP+Python) for rendering email related images and measurements. Sonifications.
- Artistic presentations: sonic skull, freakcoding.
28
Software
Official Python packages (PyPI) for precise and efficient sharing of the developments:
- Observation of circular measurements, topological stability and textual differentiation. The Percolation package.
- Routines for representing as RDF the relational data from the social participation portals ParticipaBR, Cidade Democrática and AA. The Participation package.
- Routines for representing as RDF the relational data from the social networking portals/protocols Facebook, Twitter and IRC. The Social package.
- Routines for representing as RDF the relational data from email lists in the Gmane database. The Gmane package.
- Routines rendering data visualizations with emphasis on networks. The Visuals package.
- Routines rendering music and data sonification. The Music package.
29
Conclusions
- We believe that the stability of the human interaction networks is better quantified and qualified by the invariance of the fraction of participants in each sector, the small dispersion of the principal components and the circular statistics.
- The texts produced by each sector are very different. The differences are in some cases easy to interpret from data.
- Data, ontologies and software legacy.
- Typologies derived from the analysis.
- Two published articles (not related to the thesis).
- The article on the stability of interaction networks has been accepted for publication in Physica A.
- Other articles are being submitted to journals (about power laws and music).
- Other articles are being revisited and enhanced for publication (on the textual differentiation, on ontologies, on Versinus, on the adaptation of the Kolmogorov-Smirnov two-sample text).
- Many possibilities for next steps e.g. inclusion of TF-IDF measurements, sentiment analysis, other measures of text and topology, visual analytics.
30
Bibliography
- BIRD, C. et al. Mining email social networks. In: INTERNATIONAL WORKSHOP ON MINING SOFTWARE REPOSITORIES. 2006, Shanghai. Proceedings… New York: ACM. p. 137–143, 2006.
- NEWMAN, M. Networks: an introduction. Oxford: Oxford University Press, 2010.
- COSTA, L. F. et al. Characterization of complex networks: a survey of measurements. Advances in Physics, v. 56, n. 1, p. 167–242, 2007.
- BIRD, S.; KLEIN, E.; LOPER, E. Natural language processing with Python: analyzing text with the natural language toolkit. Beijing: O'Reilly, 2009.
- BECK, F. et al. A taxonomy and survey of dynamic graph visualization. 2016.
- BERNERS-LEE, T. Linked data. 2006.
31
Thank you!